[新しいコレクション] モル比 体積比 111404-モル比 体積比 液体

原子番号 元素記号 元素名 原子量 1 H 水素 2 He ヘリウム 3 Li リチウム 6941 4 Be ベリリウム 5比 湿 q は、 d v q v U U U と定義され、 p e e p e e e q 0378 0622 0622 0622 と計算することができる。比湿や混合比は、温度や圧力が変化しても、空気塊 の混合や水蒸気の凝結、蒸発が起こらない限り保存する量である。このため、 気象学では、しばしば比湿や ④〜⑥式より、Pが2倍になればnも2倍に、Pが半分になればnも半分になる。つまり、 「圧力比＝モル比」 が成り立っている。 このとき、混合気体と気体A、混合気体と気体Bの圧力とモル数

物質量モル Mol とは モルの求め方や計算の本質を解説してみた 化学受験テクニック塾

モル比 体積比 液体

モル比 体積比 液体-質量モル濃度 mol/kg 比体積 m 3 /kg 質量分率 kg/kg (質量パーセント濃度 wt％) 基本単位の中で，太字の単位が溶液の濃度に用いられ，細字のモル体積，モル質量，及び比体積は物質の基本特性を示す単位である。 なお，青太字で示した単位を，パーセント表示する場合には，混同され易いので 4 モル分率(mol fraction) 絶対湿度、混合比、比湿は質量、体積を基準に定義された値である。 それに対し、モル分率は水蒸気と湿り空気のモル数の比を基準に定義される。定義は以下のとおり。 空気中の水蒸気の物質量()と、空気全体の物質量()との比

11 号 混合ガスの製造方法 Astamuse

 部分モル体積の必要性 例として、水(h2o)の体積をvとします。 体積vのh2oと体積vのh2oを混合すると、体積2vのh2oとなります。 この、体積の加算性について、1 molあたりの体積(モル体積)で説明することができます。 しかし、エタノール(etoh)の体積をvとして、体積vのh2oと体積vのetohを混合する日本大百科全書(ニッポニカ) 比体積の用語解説 単位質量の物体の占める体積のこと。比容ともいい、密度の逆数に等しい。比体積とその物質の原子量あるいは分子量との積はその物質1モルの占める体積であり、モル体積とよばれ、単体の場合は原子体積または原子容、化合物の場合は分子 以下の2つの基本問題のとらえ方の違いについてです。計算過程は省略しておきます。問A・・・空気を酸素と窒素の体積比が 1対4 の混合気体であるとして、 1atmの空気中の酸素と窒素の分圧を求めよ。問B・・・3Lの容器に4atmの酸

原子番号 元素記号 元素名 原子量 密度g/cm3 1 H 水素 009 2 He ヘリウム 018 3 Li リチウム 6941 053 ④〜⑥式より、Vが2倍になればnも2倍に、Vが半分になればnも半分になる。つまり、 「体積比＝モル比」 が成り立っている。 このとき、混合気体と気体A、混合気体と気体Bの体積とモル数 高校化学は何が難しいか？自分なりに考えてみる。 例題 6リットルで1×10^5 Paの酸素と2リットルで2×10^5 Paのアルゴンを混合したときの平均分子量は？(O=16,Ar=40) この短い問題を解くために知らなければならない知識は、 平均分子量はモル分率で求めにいくこと、 同温度同圧力でのモル比は分体積

(モル比 から転送) 出典 フリー百科事典『ウィキペディア（Wikipedia）』 ( 2213 UTC 版) 物質量（ぶっしつりょう、英語 amount of substance ）は、物質の量を表す物理量のひとつ である 。 物質を構成する要素粒子の個数をアボガドロ定数 (約 6022×10 23 mol1) で割ったものに等しい 。 TiO2のモル濃度が 05mol/L(1L中に05molのTiO2) ZrO2のモル濃度が 04mol/L(1L中に04molのZrO2) ですから、同体積の溶液をもってくると、5mol：4molの割合でTiとZrが入っています。 従って、5：4の逆比（＝4：5）にする、 つまりTiO2を4体積、ZrO2を5体積もってくると この混合物中の、TiZrのモル比が1：1となり 物理学 空燃比計算の意味について 熱管理士テキストの中に、「燃空比＝燃料質量／空気質量」の計算がでてきますが、ここで言う空気の質量とは、理論空気量あるいは実際の空気量を指すのでしょうか？であれば気 質問No

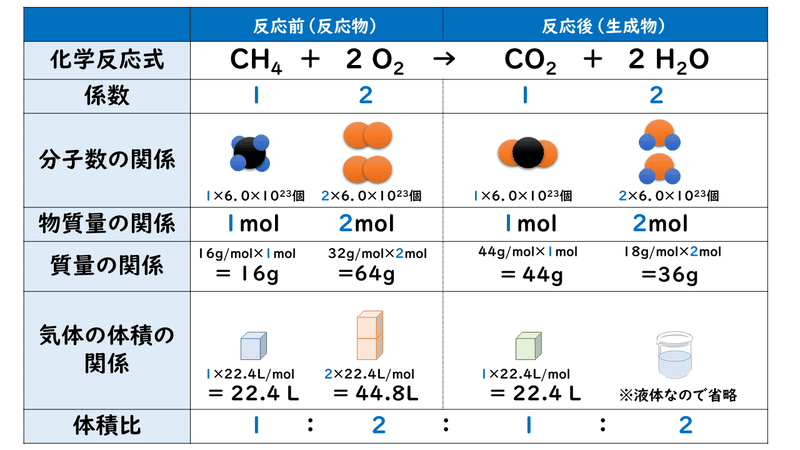
5 2 化学反応の量的関係 1 おのれー Note

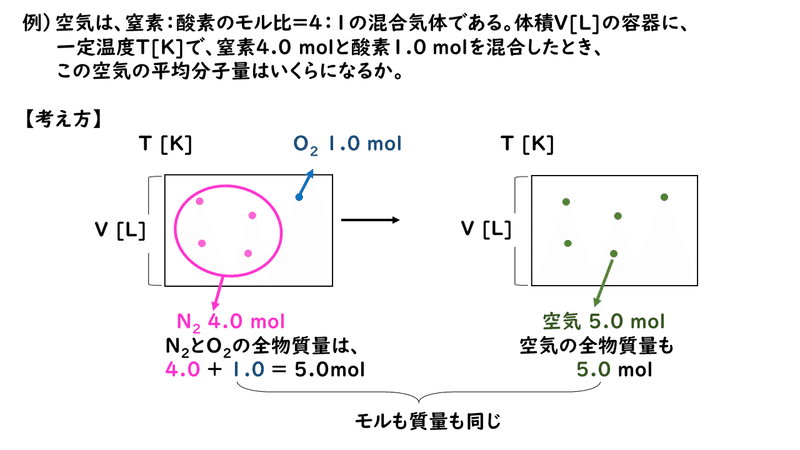
4 5 気体の密度と平均分子量 おのれー Note

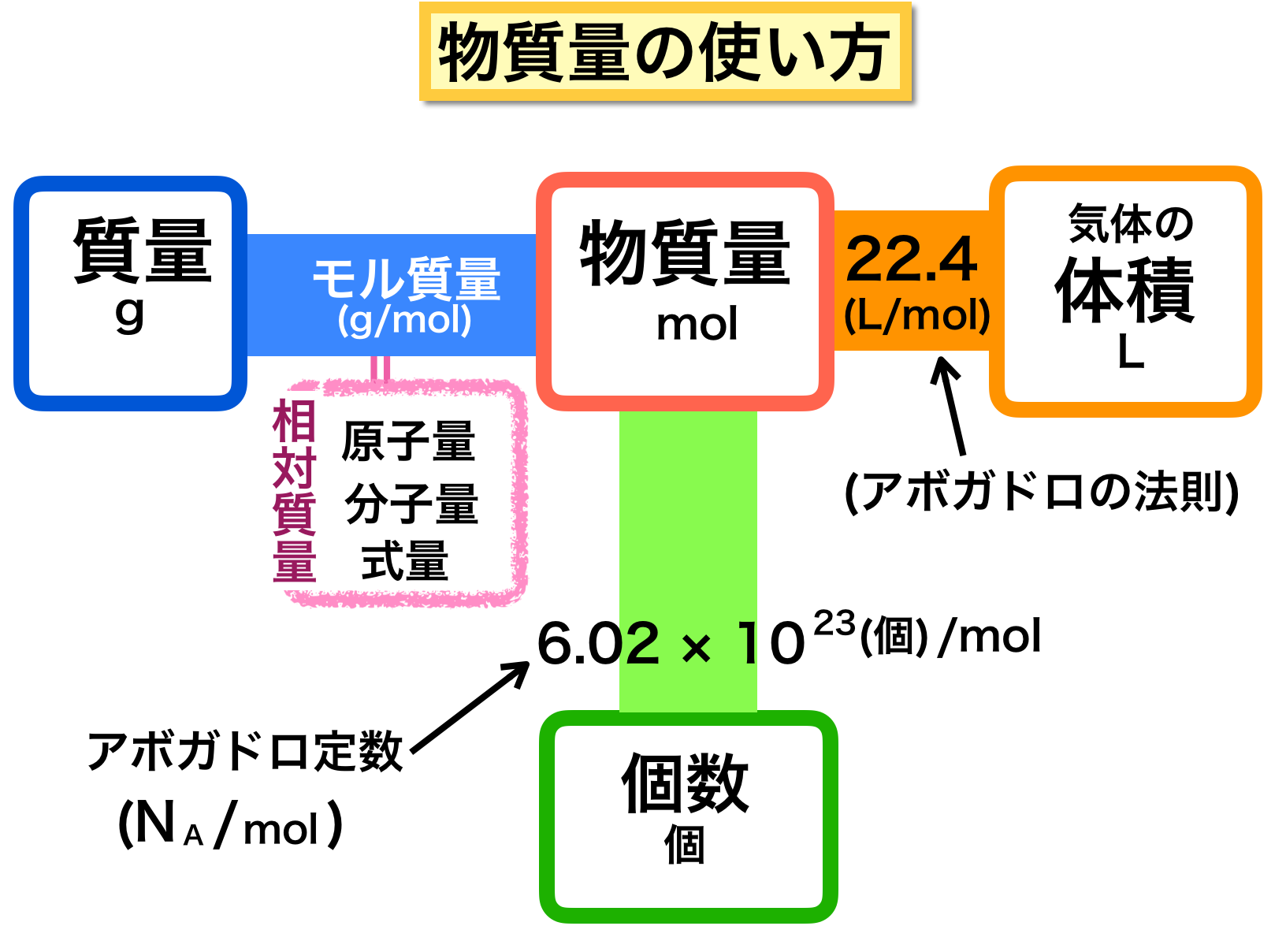
 重量比（配合比）の計算問題を解いてみよう それでは、重量比（配合比）の計算に慣れるためにも、練習問題を解いていきましょう。 ・例題1 砂糖10gと甘味料40gを混ぜて、程よい甘さでカロリーの少ないものを作りたいとします。モル体積 （モルたいせき）とは、単位 物質量 （1 mol ）の 原子 または 分子 が 標準状態 で占める体積である 。 モル質量 （ kg /mol）÷ 密度 （kg/ m 3 ）でも求められる。つまり、横軸にモル分率𝑥 F、縦軸にモル体積Vmをとると、 切片から部分モル体積𝑉 Eがわかる。 Aの部分モル 体積 Bの部分モル 体積 部分モル体積は、 混合する液体の 体積比で変わる 𝑉 E𝑉 à𝑥 F d𝑉 à d𝑥 F

物質量モル Mol とは モルの求め方や計算の本質を解説してみた 化学受験テクニック塾

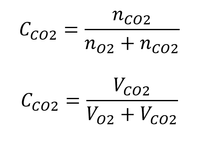
第3章

度の計算（％濃度，モル濃度）などみなさんが拒絶反応を示しそうな計算も必要です． 中学時代のつまずきを克服しないまま高校に来ている人はもちろんのこと，そうでない 人も，指数や分数を扱う計算に抵抗感をもつのではないでしょうか？そのあたりの漠然と した不安感に光をあて，「なモル体積とは、気体物質1mol当たりの体積のことをいい、気体の種類にかからわず、標準状態で224L/mol 上記にあるように、 化学反応式の係数比はモル比 と等しい。 問題文に完全に反応が進行したとあるので 水素か酸素のどちらかが完全になくなるまで反応が進んだ ことになる。 水素と酸素比熱容量J/kg・K 比熱比κ 定圧比熱c p 定積比熱c v c p /c v 1 He 4 5192 3116 166 2 O 2 32 9 659 140 3 以上 CO 2 44 844 655 129 NH 3 17 51 1570 131 CH 4 16 2228 1710 130 表25℃における気体の定圧・定積比熱、比熱比 法則性はある?

同温 同圧では物質量の比は体積比とはどういう意味ですか モル分率は成 Yahoo 知恵袋

モル比 体積比 いいとこだよなぁ 三重って

解決手段Ba／Tiモル比が1．01〜1．18であり、950〜1100℃の温度で焼結されるチタン酸バリウム（BaTiO 3 ）焼結体用原料粉末。 効果950〜1100℃という低温での焼結によって、嵩密度の高いチタン酸バリウム焼結体を得ることができる。化学反応式においては、気体の体積の比=物質量の比 最後に、 気体の体積 を考えましょう。 気体の体積の求め方を覚えていますか？ 気体はその種類に関係なく、（標準状態においては） 1molあたり224L でした。 ということは、C 3 H 8 の体積は、1×224=224Lとなります。 O 2 の体積は密度＝質量／体積＝モル質量／モル体積（化学基礎） 密度とは、その物質が他の物質に比べて重いか軽いかをしめす値です。 例えば金はアルミニウムよりも密度が大きい。 金とアルミニウムを同じ体積（容量）だけ集めたら、金のほうがアルミニウム

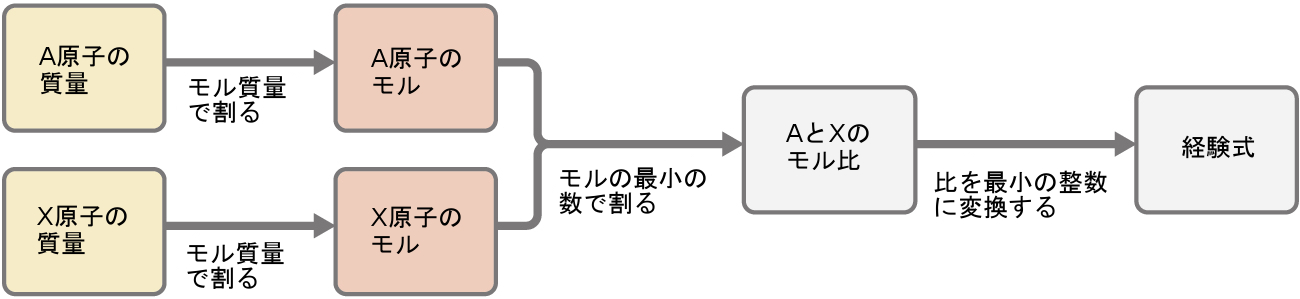
第3章 物質と溶液の組成 化学 第2版

分圧比 モル比 体積比とかいてあるのですが 左ページの一番下の問 Yahoo 知恵袋

同温，同圧で，互いに反応する気体の体積間には簡単な整数比が 2モルあたりの質量が最も大きい物質を，次の① 〜 ⑤のうちから一つ選べ。 ① 酸素 ② 水 ③ アンモニア ④ 塩化水素 ⑤ 水酸化カルシウム 類題 4 ① 1molの水素があります。この水素の質量はいくらでしょうか。 ② 水が24また、断熱変化において、圧力p，体積Vの間には、 という関係がある。この式をポアッソンの関係式と言う。γ は、比熱比 である。 断熱変化のp－V図は、等温曲線よりも傾きが急になる。 断熱変化においては、気体が吸収した熱は0で、気体のした仕事をW，内部エネルギーの変化を として、熱 最終更新日 wt％とは「重さで考えたときの濃度」 vol％とは「体積で考えたときの濃度」 mol％とは「物質量（モル）で考えたときの濃度」 濃度を表す3つの方法（wt％、vol％、mol％）について、それぞれ意味と計算例を解説します。

分圧の法則と計算問題 理系ラボ

物質量molの超解説 理系ラボ

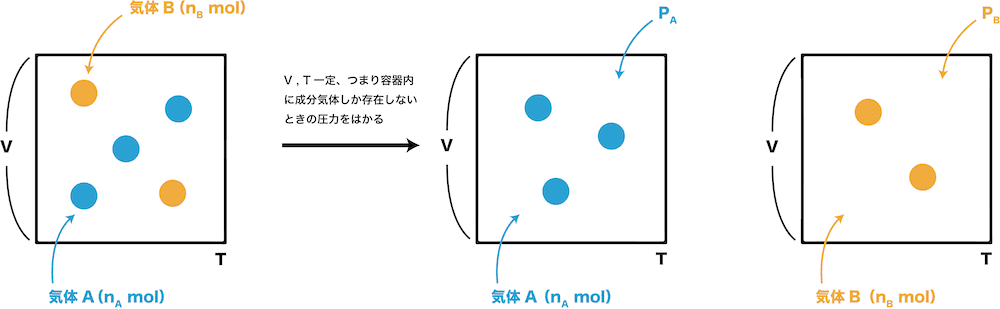
となる。ここで、体積比はモル数比に等しい、V 1 /V a = n 1 /n a 、ということ（13行目）であるが、体積V 1 を持っていた気体1の体積は、混合後にはV a になっているため、すでに混合された気体についてV 1 を考えることは難しい。 1＝10MPa の飽和水蒸気の比体積v 1 ''，t 2＝60℃の飽和水蒸気の比体積v 2 ''，飽和水の 比体積v 2 'を求めよ。 (2) 放熱後の湿り飽和水蒸気の乾き度x を求めよ。 (3) この過程での放熱量Q を求めよ。 (1) 飽和蒸気表から次のように求められる。 v 1 ''＝m 3/kg (答体積（v）と温度（t）が同じであり、気体定数（r）は常に一定のため圧力（p）とモル（n）は比例関係にあることがわかります。 つまり温度と体積が変わらない条件で、例えば 気体 A と気体 B のモル比が 4 1 で混ざっているとき、 気体の分圧も 4 1 になるということです。

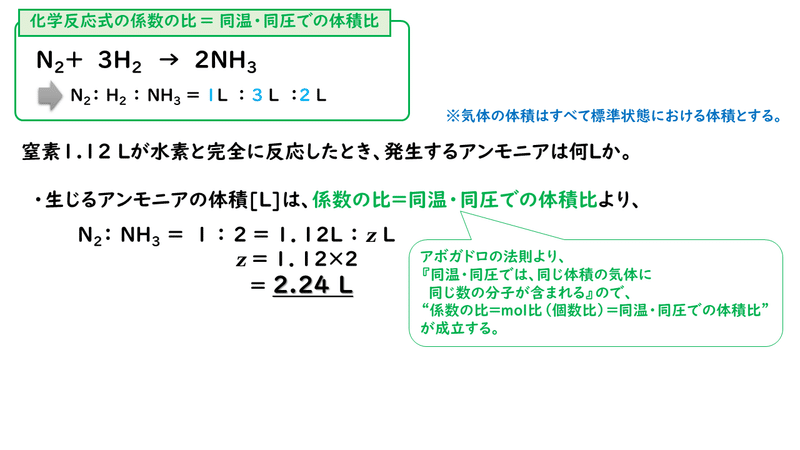
5 2 化学反応の量的関係 1 おのれー Note

第９５章 混合気体

質量比（重量比）・モル比（物質量比）・モル質量の換算の計算問題を解いてみよう 二成分系の混合気体における質量比とモル比の変換（換算）の計算を行っていきましょう。 例題 ある容器内に酸素と水素がモル比15で入っているとします。モル比は、 化学反応に関与する任意の2つの化合物の モル量の比である 。 モル比は、多くの化学的問題において生成物と反応物との間の変換係数として使用される 。 モル比は、バランスのとれた化学式の式の前の係数を調べることによって決定することが 分圧比＝モル比 (体積、温度が一定の時) 体積比＝モル比 (圧力、温度が一定の時) というのは、理解できるのですが。 圧力の比＝体積の比 というふうに直接結びつけるとなると 条件として、何が一定でないとダメなのか、よくわかりません

混合気体について 混合気体について 高校化学の混合気体について わから Okwave

15 旧課程第1問 問5 化学反応式と体積変化 化学がちょっとだけ好きな社労士

 モル比と体積比が等しいのは知ってますが、モル比と質量比、モル比と構成粒子の個数の比（分子の数など）は等しいのですか？ 化学 下の化学の問題、リン酸の滴定の問題について質問です。 問題では、『点cにおけるphを求めよ』と言われているんですけど、さっぱりわかりません

本田塾 気体マスターコース 3日間 2時間 オンライン Coubic

高校化学基礎 化学反応式と係数 映像授業のtry It トライイット

ヘンリーの法則まとめ 公式 体積 問題 理系ラボ

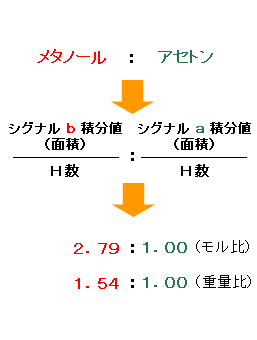
Nmrによる定量分析 株式会社ube科学分析センター

質量分率と体積分率の変換 換算 方法 計算

気体の平衡の計算 問題と答え 大学受験の王道

15 旧課程第1問 問5 化学反応式と体積変化 化学がちょっとだけ好きな社労士

11 号 混合ガスの製造方法 Astamuse

空気中では 体積比 モル比 になるのですか この時圧力は大気圧な Yahoo 知恵袋

分圧の法則と計算問題 理系ラボ

物質量 求め方

高2 化学基礎 化学反応式です 解き方から書いてもらえると嬉しいです Clearnote

化学基礎 物質量の計算問題 標準状態の気体の体積と物質量の関係 比の活用など Youtube

ある程度基礎が身についたら Molの比 気体体積の比 は使ってよい 化学がちょっとだけ好きな社労士

5 2 化学反応の量的関係 1 おのれー Note

化学 プロパンの燃焼 空気は何ｌ Youtube

2 の で体積一定のとき 分圧比と物質量比が等しいとありますが3 で 化学 教えて Goo

Woa1 Silver Powder Mixture Method For Producing Same And Conductive Paste Google Patents

ドルトンの分圧の法則と混合気体の状態方程式

比容積 それが意味することとそれを計算する方法

Y Katsura Starrydata E4mでは 元素の周期表にいろいろな物性データを表示するツールも作りました プルダウンから配色と物性名 英語 を選択すると 周期表上に色と数値で各元素の物性値を表示してくれます 元素の物性データは機械学習用の元素記述子

同温 同圧では物質量の比は体積比とはどういう意味ですか モル分率は成 Yahoo 知恵袋

気体の性質 混合気体の反応後の量を求める過程がわかりません 化学 定期テスト対策サイト

Y Katsura Starrydata E4mでは 元素の周期表にいろいろな物性データを表示するツールも作りました プルダウンから配色と物性名 英語 を選択すると 周期表上に色と数値で各元素の物性値を表示してくれます 元素の物性データは機械学習用の元素記述子

分体積 全体積 化学のグルメ

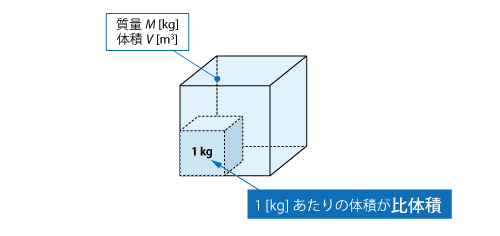
比体積

高校化学の気体の問題です 若干複雑ですが 回答していただけると嬉しいです Clearnote

質量比 重量比 と体積比 容積比 の変換 換算 の計算問題を解いてみよう 混合気体

体積比 容積比 とモル比 物質量比 が一致する理由 定積 定温下

化学反応におけるモル比は何ですか

Wo06 号 アルミニウム系材料のろう付け用フラックス粉末及び該フラックス粉末の製造方法 Astamuse

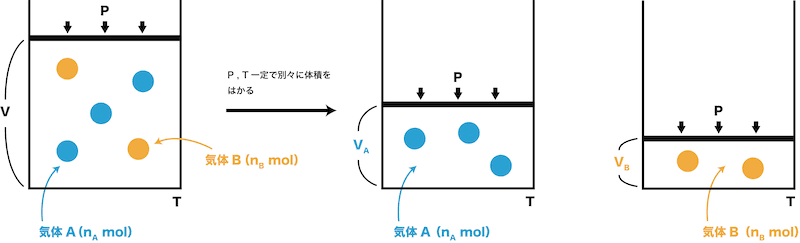
分体積 全体積 化学のグルメ

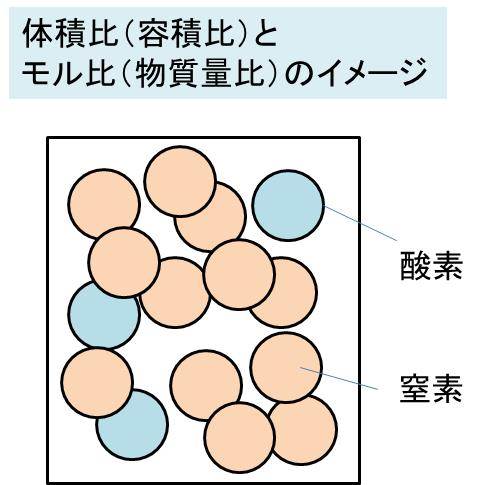
体積比 容積比 とモル比 物質量比 が一致する理由 定積 定温下

5 2 化学反応の量的関係 1 おのれー Note

モル比 体積比 分圧比とあるのですが分圧は同じ体積で考えて 体積も同じように同 Yahoo 知恵袋

11 号 混合ガスの製造方法 Astamuse

化学基礎 解き方教えてください Clear

モル比と重量比について質問です H2oのモル比と重量比 Yahoo 知恵袋

どうして 酸素と窒素の体積比が1 4だと5をかけるのですか Clearnote

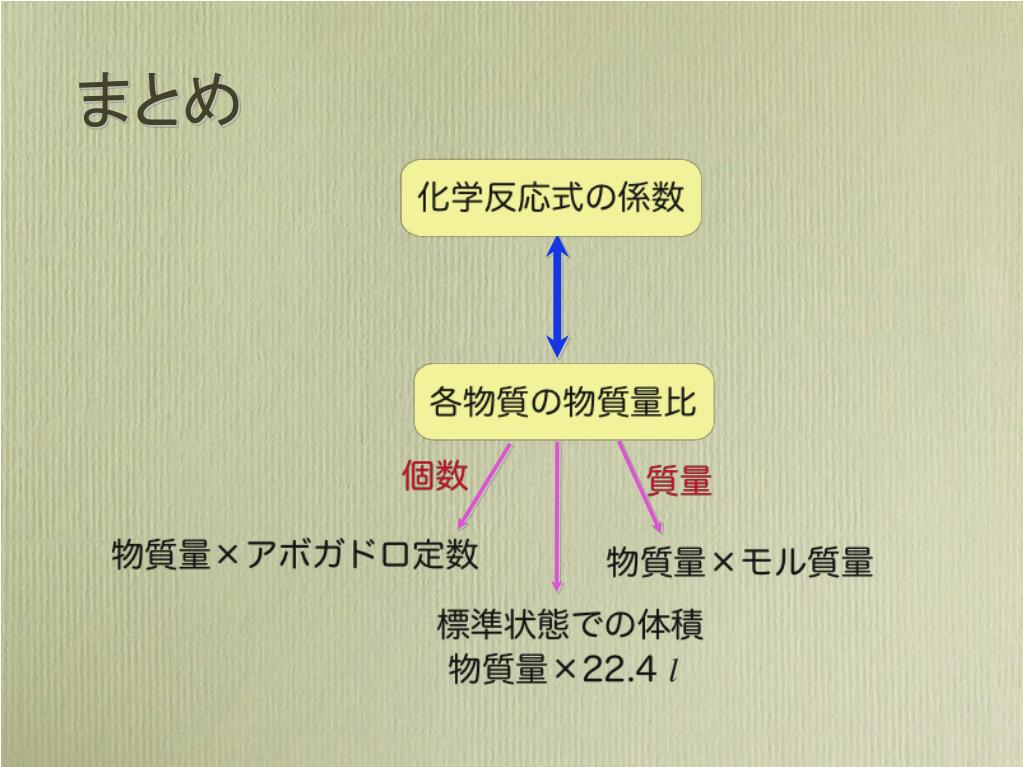
Ppt 化学反応式 Powerpoint Presentation Free Download Id

令和版 合格報告あり 丙種液石問題集 学識 比体積 質量の計算 過去問と音声テキストを公開 資格勉強を全力で応援

高校化学基礎 化学反応式と係数 映像授業のtry It トライイット

モル比 分体積比証明 化学受験テクニック塾

気体の平衡の計算 問題 大学受験の王道

17 号 マグネシア系触媒担体及びその製造方法 Astamuse

ドルトンの分圧の法則と混合気体の状態方程式

気体の性質 混合気体の反応後の量を求める過程がわかりません 化学 定期テスト対策サイト

この問題２３について質問です 自分はこの問題を 化学反応式からモル比 その他 教育 科学 学問 教えて Goo

の全圧をモル比を利用して出したのですが 解答の のvについての説明がよく分 Clearnote

分体積 全体積 化学のグルメ

Htracyhall Org

係数比 Mol比 気体の体積比 分圧の比 化学がちょっとだけ好きな社労士

係数比 Mol比 気体の体積比 分圧の比 化学がちょっとだけ好きな社労士

5分でわかる 分圧 全圧との違いは 混ざっているのに圧力は分けられる 元研究員がわかりやすく解説 ページ 2 2 Study Z ドラゴン桜と学ぶwebマガジン

物質量比 体積比 分圧比なのですか 違うとしたらどのようになるのですか Yahoo 知恵袋

Wo06 号 アルミニウム系材料のろう付け用フラックス粉末及び該フラックス粉末の製造方法 Astamuse

混合気体の分圧 分体積の計算法 史上最強の解法がここに 化学受験テクニック塾

化学に関して質問です 体積比がどうして物質量比といえるのでしょうか また 物質 Yahoo 知恵袋

Ppt 化学反応式 Powerpoint Presentation Free Download Id

2

分圧 全圧 モル分率 化学のグルメ

Y Katsura Starrydata E4mでは 元素の周期表にいろいろな物性データを表示するツールも作りました プルダウンから配色と物性名 英語 を選択すると 周期表上に色と数値で各元素の物性値を表示してくれます 元素の物性データは機械学習用の元素記述子

化学反応式 係数 作り方 書き方 計算問題の解き方など 化学のグルメ

問題 の操作1でａは温度と圧力が一定だから体積比はモル比になると解説 化学 教えて Goo

物質量比 体積比 分圧比なのですか 違うとしたらどのようになるのですか Yahoo 知恵袋

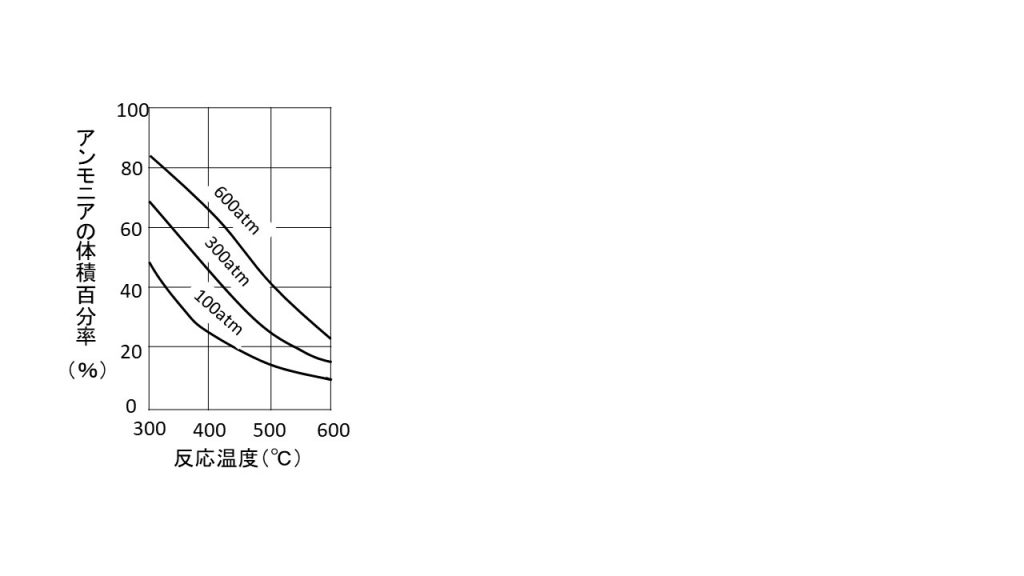
大気の平均分子量と物質量 Mol のまとめ 色と形で気象予報士

混合気体の分圧 分体積の計算法 史上最強の解法がここに 化学受験テクニック塾

Nasa Cea

モル比 体積比 分圧比とあるのですが分圧は同じ体積で考えて 体積も同じように同 Yahoo 知恵袋

5 2 化学反応の量的関係 1 おのれー Note

15 第3問 問5 混合物の物質量の比 化学がちょっとだけ好きな社労士

高校化学基礎 化学反応式と係数 映像授業のtry It トライイット

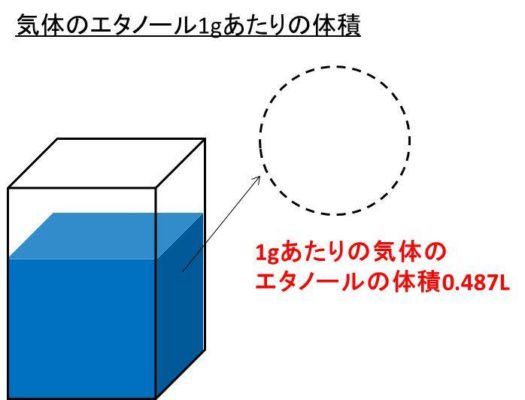
エタノール アルコール が気体に変わると体積は何倍になるのか 体積比 体積膨張率 の計算 白丸くん

2

تويتر マナ物理 على تويتر 気体の混合 その２ 添付ファイル 4枚 の問題を解いてください ボイル シャルルの法則 は 体積や圧力の単位が多く登場する 化学 では使える法則として活躍しますが 物理 では必要ないです 熱力学において ある瞬間 に

1

Woa1 Positive Electrode For Lithium Secondary Batteries And Lithium Secondary Battery Using Same Google Patents

物質量molの超解説 理系ラボ

Nasa Cea

空気中では 体積比 モル比 になるのですか この時圧力は大気圧な Yahoo 知恵袋

混合気体の分圧 分体積の計算法 史上最強の解法がここに 化学受験テクニック塾

ドルトンの分圧の法則と混合気体の状態方程式

金属モル比の意味 用法を知る Astamuse

物質量比 体積比 分圧比なのですか 違うとしたらどのようになるのですか Yahoo 知恵袋

モル比は 英語 意味 英語訳 日本語の例文

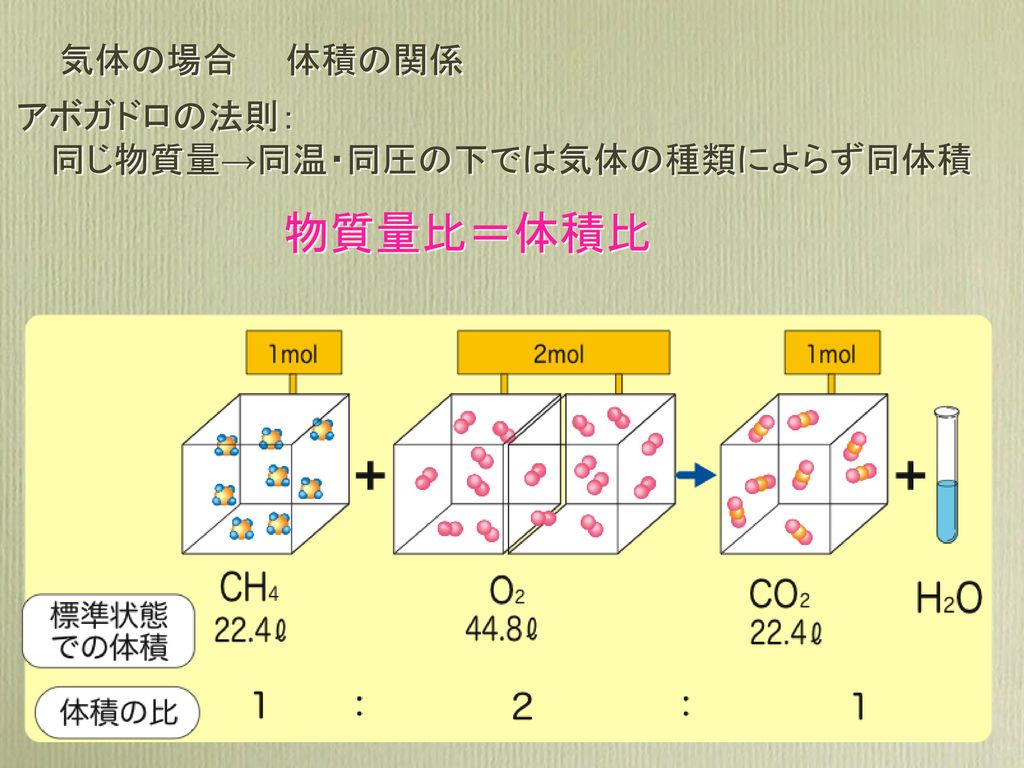
化学反応式 化学反応 ある物質が別の物質に変化 反応物 生成物 例 酸素と水素が反応して水ができる 反応物 酸素と水素 生成物 水 Ppt Download

1

化学反応式 係数

3 なのですが O2とh2oの体積比から求めることはできないのでしょうか Clearnote

高校理論化学 化学反応式と化学反応の量的関係 過不足のある反応 混合気体の燃焼 混合物の純度 受験の月

Incoming Term: モル比 体積比, モル比 体積比 液体,